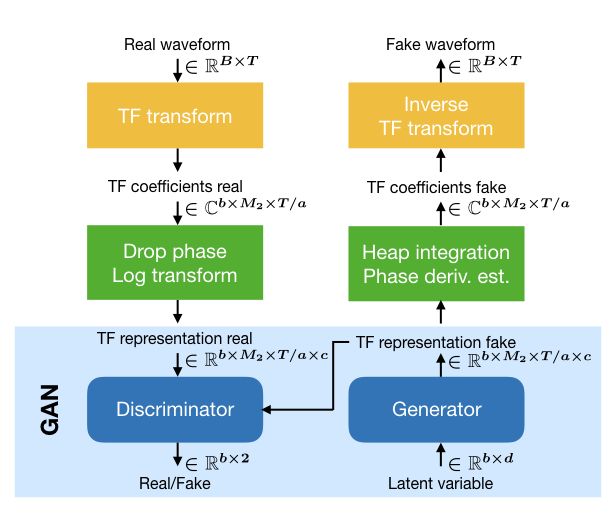
Time-frequency (TF) representations provide powerful and intuitive features for the analysis of time series such as audio. But still, generative modeling of audio in the TF domain is a subtle matter. Consequently, neural audio synthesis widely relies on directly modeling the waveform and previous attempts at unconditionally synthesizing audio from neurally generated TF features still struggle to produce audio at satisfying quality. In this contribution, focusing on the short-time Fourier transform, we discuss the challenges that arise in audio synthesis based on generated TF features and how to overcome them.

We demonstrate the potential of deliberate generative TF modeling with TiFGAN, which generates audio successfully using an invertible TF representation and improves on the current state-of-the-art for audio synthesis with GANs. TiFGAN is an adaptation of DCGAN, originally proposed for image generation. The TiFGAN architecture additionally relies on the guidelines and principles for generating short-time Fourier data that we presented in the accompanying paper.

The general architecture for TiFGAN is depicted above. For the purpose of this contribution, we restrict to generating 1 second of audio data, sampled at 16kHz. For the short-time Fourier transform, we chose for the analysis window a (sampled) Gaussian and fix the minimal redundancy that we consider reliable, i.e., M/a = 4 and select a=128, M=512. Since the Nyquist frequency is not expected to hold significant information for the considered signals, we drop it to arrive at a representation size of 256x128, which is well suited to processing using strided convolutions. For the reconstruction of the phase we use phase-gradient heap integration (PGHI) (see Prusa et Al) which requires no iteration, such that reconstruction time is comparable to simply integrating the phase derivatives. For synthesis from the STFT, we use the canonical dual window, precomputed using the Large Time-Frequency Analysis Toolbox (LTFAT).

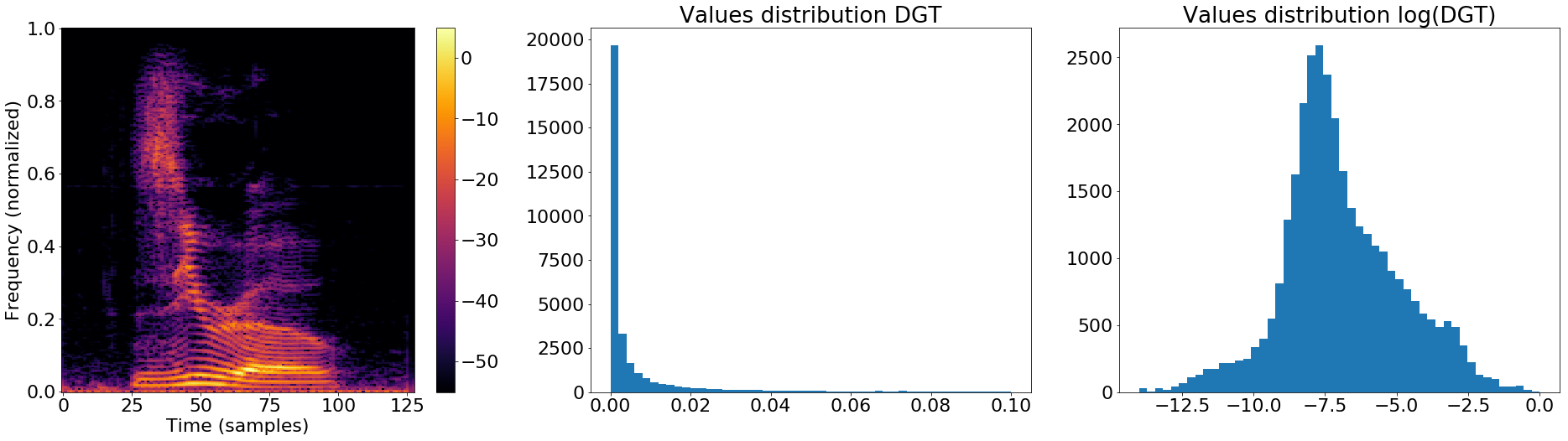
Since the distribution of values in the magnitude of the Short-Time Fourier Transform (STFT) is not well suited for a GAN (see Figure above) we use log-magnitude coefficients. We first normalize the STFT magnitude to have maximum value 1, such that the log-magnitude is confined in (-inf, 0]. Then, the dynamic range of the log-magnitude is limited by clipping at -r (in our experiments r=10), before scaling and shifting to the range of the generator output [-1,1], i.e. dividing by r/2 before adding constant 1.

The network trained to generate log-magnitudes will be referred to as TiFGAN-M. For TiFGAN-M, the phase derivatives are estimated from the generated log-magnitude. Generation of, and synthesis from, the log-magnitude STFT is the main focus of this contribution. Nonetheless, we also trained a variant architecture TiFGAN-MTF for which we additionally provided the time- and frequency-direction derivatives of the (unwrapped, demodulated) phase.

Different phase recovery strategies

Overview of spectral changes resulting from different phase reconstruction methods. (1) Original log-magnitude, (2-4) log-magnitude differences between original and signals restored with (2) cumulative sum along channels (initialized with zeros), (3) PGHI from phase derivatives (4) PGHI from magnitude only and phase estimated from the phase-magnitude relations.

It may seem straightforward to restore the phase from its time-direction derivative by summation along frequency channels as proposed by Engel et Al. Even on real, unmodified STFTs, the resulting phase misalignment introduces cancellation between frequency bands resulting in energy loss, see Figure above (2) for a simple example. In practice, such cancellations often leads to clearly perceptible changes of timbre (see below). Moreover, in areas of small STFT magnitude, the phase is known to be unreliable (see Balazs et Al) and highly sensitive to distortions (see Alaifari et Al), such that it cannot be reliably modelled and synthesis from generated phase derivatives is likely to introduce more distortion.

Phase-gradient heap integration (PGHI) (see Prusa et Al) relies on the phase-magnitude relations and bypasses phase instabilities by avoiding integration through areas of small magnitude, leading to significantly better and more robust phase estimates see Figure above (4). PGHI often outperforms more expensive, iterative schemes relying on alternate projection, e.g., Griffin-Lim, at the phaseless reconstruction (PLR) task.

The following examples were computed on samples from the EBU SQAM dataset.

• Original
• Phase from the time-direction derivative
• Phase from PGHI

• Original (2)
• Phase from the time-direction derivative (2)
• Phase from PGHI (2)